Algorithmus - Liegt ein Punkt in einem Polygon?

Kurzbeschreibung

Dieser Algorithmus berechnet, ob ein Punkt in einem Polygon liegt (2D). Der Punkt ist ein X/Y-Koordinatenpaar des Typs stc_Point. Das Polygon ist ein Array, das ebenfalls aus einzelnen Punkten (stc_Point) besteht. In der derzeitigen Implementierung sind nur "gewöhnliche" Polygone möglich; also keine, deren Umfangslinien sich selbst schneiden.

Erstellt wurde dieser Algorithmus u.a. für einen Microcopter, um in bestimmten Bereichen eine Höhenbegrenzung bzw. Mindesthöhe festzulegen. Somit kann man verhindern, dass der Microcopter z.B. über einer Wasserfläche eine Landung zulässt. Ebenso kann man auch bestimmte erhabene Hindernisse festlegen.

Alle 4 Winkel (jeder ungleich ∏) ergeben 2∏; Punkt liegt somit im Polygon

Einer der Winkel (hier γ) ist ∏: Punkt liegt auf einer Kante

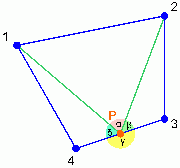
Einer der Winkel (hier δ) ist >∏. Da alle Winkel <= ∏ sein müssen, wird von δ 2∏ abgezogen. Winkelsumme damit 0: Punkt liegt ausserhalb

Erklärung

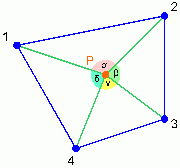
Vom zu prüfenden Punkt aus werden Geraden zu den Eckpunkten des Polygons gezogen. Zwischen diesen Geraden wird die Summe aller Winkel berechnet (vgl. auch Windungszahl).

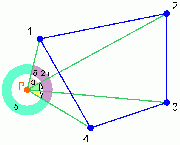
Ist die Winkelsumme +/-2∏ (+/-360°, Windungszahl +/-1), liegt der Punkt im Polygon. Ist die Winkelsumme 0, liegt der Punkt ausserhalb. Der Sonderfall, dass der Punkt auf einer Kante liegt, wird dadurch erkannt, dass einer der Einzelwinkel +/-∏ (+/-180°) ist. Den Sonderfall, dass der Punkt auf einem anderen Polygon-Eckpunkt liegt, kann man einfach erkennen, in dem man überprüft, ob der Punkt einem der Polygonpunkte entspricht.

Update 2014-05-01

Die bisher verwendete Abfrage im Code, ob die Winkelsumme 0 bzw. +/-2∏ + etwas Toleranz durch die Rundungsfehler beträgt, wurde optimiert. Da die Winkelsumme ja nur 0 oder +/-2∏ annehmen kann, wird einfach der Betrag der Winkelsumme mit ∏ verglichen. Ist der Betrag kleiner, muss die Winkelsumme 0 sein. Ist er grösser, kann die Winkelsumme nur +/-2∏ sein.

Funktionen

PointInPolygon

• stc_Point P_loc: Zu prüfender Punkt
• stc_Point *Polygon: Zeiger auf Array mit den Punkten des Polygons
• uint8_t PolygonSize: Anzahl der Punkte des Polygons

• PiP_Corner: Punkt liegt auf einem Eckpunkt des Polygons
• PiP_Edge: Punkt liegt auf einer Kante des Polygons
• PiP_Outside: Punkt liegt ausserhalb des Polygons
• PiP_Inside: Punkt liegt innerhalb des Polygons
• PiP_Unknown: Unerwartetes Ergebnis; sollte nie vorkommen

Code

#include <math.h>
#include <stdlib.h>
 
typedef enum{
  PiP_Unknown = -3,
  PiP_Corner  = -2,
  PiP_Edge    = -1,
  PiP_Outside =  0,
  PiP_Inside  =  1
} e_PiP_result;
 
typedef struct{
  int32_t x;
  int32_t y;
} stc_Point;
 
e_PiP_result PointInPolygon(stc_Point P_loc, stc_Point *Polygon, uint8_t PolygonSize)
{
  uint8_t   pcnt;         // Counter for polygon points
  stc_Point P1;           // Point Pn for angle calculation
  stc_Point P2;           // Point P_loc for angle calculation
  stc_Point P3;           // Point Pn+1 for angle calculation
  stc_Point V_P2P1;       // Vector P_loc -> Pn
  stc_Point V_P2P3;       // Vector P_loc -> Pn+1
  double    angle;        // Angle between vectors above
  double    anglesum = 0; // Angle sum
 
  P2 = P_loc; // P2 is always the point to check
 
  // check, if point is one of the polygon points
  for (pcnt = 0; pcnt < PolygonSize; pcnt++)
  {
    if ((Polygon[pcnt].x == P2.x) && (Polygon[pcnt].y == P2.y))
    {
      // Point to check is polygon point
      return PiP_Corner;
    }
  }
 
  for (pcnt = 0; pcnt < PolygonSize; pcnt++)
  {
    // P1 = Pn
    P1 = Polygon[pcnt];
    if (pcnt < (PolygonSize-1))
    {
      // P3 = Pn+1
      P3 = Polygon[pcnt+1];
    }
    else
    {
      // on last Pn, set Pn+1 = P0 and close polygon
      P3 = Polygon[0];
    }
 
    // Get vector P2P1
    V_P2P1.x = P1.x - P2.x;
    V_P2P1.y = P1.y - P2.y;
 
    // Get vector P2P3
    V_P2P3.x = P3.x - P2.x;
    V_P2P3.y = P3.y - P2.y;
 
    // Calculate angle between vectors
    angle = atan2(V_P2P3.y, V_P2P3.x) - atan2(V_P2P1.y, V_P2P1.x);
 
    if ((angle == M_PI) || (angle == -M_PI))
    {
      // if one of the angle is +/-PI, the point is on an edge
      return PiP_Edge;
    }
 
    // maintain definition range / "limit" angles to range from ]-PI;+PI[
    if (angle < (-M_PI))
    {
      angle += (2*M_PI);
    }
    else if (angle > (+M_PI))
    {
      angle -= (2*M_PI);
    }
    anglesum += angle;
  } // END: for (pcnt = 0; pcnt < PolygonSize; pcnt++)
 
  // The possible values for anglesum are 0 or +/- 2 PI, so we
  // simply need to check, if the absolute value is less or greater than PI
 
  if (abs(anglesum) < M_PI)
  {
    return PiP_Outside;
  }
  else if (abs(anglesum) > M_PI)
  {
    return PiP_Inside;
  }
 
  // we should never land here; but when, we have a separate value for this case
  return PiP_Unknown;
}

Beispiel

Hier ein kleines Beispiel zur Verwendung. Für ein Polygon myPolygon mit 5 Punkten werden 4 verschiedene Fälle geprüft, die die jeweiligen Ergebnisse zurückgeben.

stc_Point  myPolygon[] = {
  {450, 200},
  {490, 310},
  {330, 380},
  {220, 275},
  {295, 105},
};
 
stc_Point P_innen  = { 350, 250 }; // Punkt liegt innerhalb
stc_Point P_aussen = {   0, 150 }; // Punkt liegt ausserhalb
stc_Point P_kante  = { 470, 255 }; // Punkt liegt auf einer Kante
stc_Point P_eck    = { 330, 380 }; // Punkt liegt auf einem Eckpunkt
 
int main(void)
{
  uint8_t result_innen  = PointInPolygon(myP_innen,  myPolygon, sizeof(myPolygon) / sizeof(stc_Point));
  uint8_t result_aussen = PointInPolygon(myP_aussen, myPolygon, sizeof(myPolygon) / sizeof(stc_Point));
  uint8_t result_kante  = PointInPolygon(myP_kante,  myPolygon, sizeof(myPolygon) / sizeof(stc_Point));
  uint8_t result_eck    = PointInPolygon(myP_corner, myPolygon, sizeof(myPolygon) / sizeof(stc_Point));
  return 0;
}